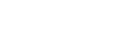1. Introduction
Whole-History Rating (WHR), is an algorithm created by Rémi Coulom in 2008 in his paper, Whole-History Rating: A Bayesian Rating System for Players of Time-Varying Strength [1]. Rémi Coulom is a French AI scientist, the author of Crazy Stone, and the founder of Kayufu. In the WHR algorithm, the complete historical game records with time information are used as input, to fit the player ratings at different time slots in their active periods. WHR has been applied to many different games, the most famous of which is the unofficial Go Ratings maintained by Rémi Coulom himself.
Now WHR has also been used to compute the ratings of renju players in the world, which can be seen here:
https://renjurating.wind23.com/
The code of WHR renju rating has been open-sourced at Github:
https://github.com/wind23/whr_renju
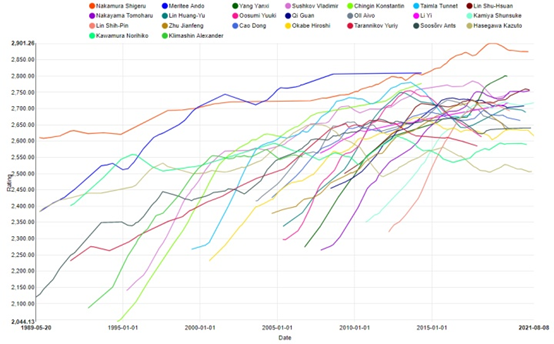
As of September 12, the top 20 players in the WHR renju rating list are shown like this:
On the website, you can see the historical changes in the rating of each player in a chart. The following figure shows the rating of the Japanese legendary player, Nakamura Shigeru, from 1988 to 2021.

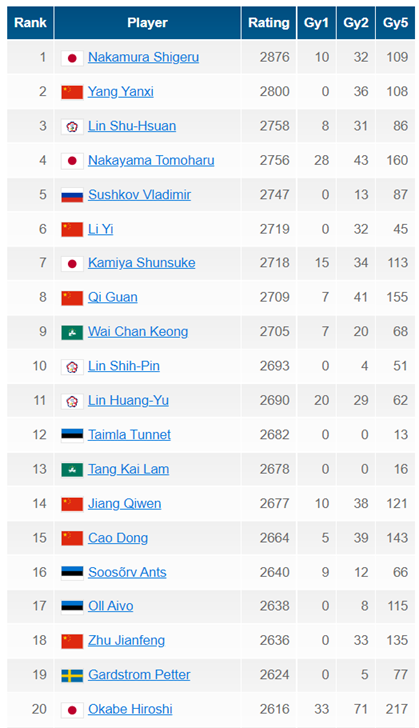
You can also see the curves of different top players in the world in the same chart. In this chart, you can see how the ratings of the top renju players change in the recent 30 years.
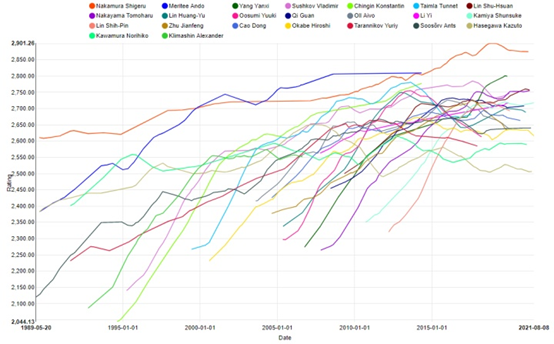
In this article, we will briefly introduce the theory of WHR, and compare it with the classical Elo rating model.
2. Elo Rating Model
The Elo rating model [2] is a classical way of computing ratings of players, and has been used in many different rating systems. It has been used by the Renju International Federation so far, which is published at:
http://renjuoffline.com/renju-rating/
Here we will briefly introduce this system first. The Elo rating system is an algorithm to compute the rating incrementally. At first, the initial ratings of players are calculated in some particular way. After that, all the game records are traversed in time order. For each game, the ratings of the two players are either increased or decreased according to the game result with a formula, in order to update the ratings incrementally.
At first, each player can get the established rating after he has played 10 games with established players, and got at least 3 points from these games. For player A, when he meets the conditions of getting an established rating, his initial rating is RA computed as:

Here Rm is the average rating of all his established opponents, W and L are the numbers of his wins and losses, and n is the number of all such games.
After a player gets his established rating, his rating is updated with an incremental formula. It is based on the Bradley-Terry model. For player A and B, and a game g between them, the expectation of the score player A gets is computed as:
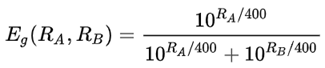
When the result of game g is Sg (the value of Sg is 1 for a win, 0.5 for a draw, and 0 for a loss for player A), the new rating of player A is computed as:

Similarly, the new rating of player B is computed as:
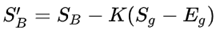
In this way, after we go through all the game records to update the ratings, we can get the final ratings of all players.
3. WHR algorithm
WHR is different from the classical Elo rating model where the ratings are updated incrementally. In WHR, each player is assigned a rating as a variable at each time point. These variables are used to construct a probabilistic model, and computed together to get the ratings of all players at all time points, in order to optimize the objective function of the probabilistic model. One of the most important assumptions of WHR is, for player A with two ratings RA(t1) and RA(t2) at two different time points t1 and t2, the closer t1 and t2 are, the more relative ratings RA(t1) and RA(t2) would be. It implies a fact that is consistent with our experience: the rating of a player usually does not change abruptly within adjacent time points.
Similar to the classical Elo rating system, the ratings computed with WHR satisfy a dynamic version of the Bradley-Terry model. For game g between player A and player B at time t, assume their ratings are RA(t) and RB(t) at time t. According to the Bradley-Terry model, the expectation score player A gets will be:
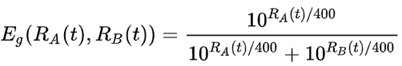
As described, the WHR model assumes that a player would have similar scores at adjacent time points. For RA(t1) and RA(t2), when t2>t1, RA(t2) follows a Gaussian distribution with the center point to be RA(t1):

Here w is a hyperparameter showing the changing rate of player ratings. A higher value of w indicates that the ratings of players would change more abruptly over time. Given the above distribution, when the value of r1= RA(t1) is fixed, the probability density function of RA(t2) will be:

Here σ=w(t2–t1)1/2.
Following the above assumptions, we have the following probabilities: (i) For each game, the probability that the result predicted by the Bradley-Terry model is consistent with the truth. This probability is equal to pA=Eg(RA(t),RB(t)) when A wins B, pB=1-Eg(RA(t),RB(t)) when B wins A, and (pApB)1/2 when there is a draw. (ii) For each player and each pair of adjacent time points t1 and t2, the probability density p(r2|r1).
Multiplying the above probabilities, we get a function with the inputs to be the ratings of all players at all valid time points Rp(t). Assume that R is the set of all these historical ratings, and G is the set of all games. According to the Bayes’ law, given the set of all games G, the probability density of ratings R will be:

Here p(G) is a constant, p(G|R) is the product of all the elements in (i), and p(R) is the product of all the elements in (ii). In the above equation, the only set of variables are R. Thus, as long as we compute the values of R which maximize the value of the objective function p(R|G), we get the ratings of all players at all time points in the same time. By iterating with the Newton’s method, we can get the solution to the problem. If you are interested, you can refer to the open-source code for the detailed algorithm on Github. In conclusion, in the WHR model, given the existing history game records, we can find the player ratings that can maximize the likelihood that the existing game records become true, which are considered as our final output.
4. Comparison between two Systems
Compared with WHR, the Elo rating model is simpler and easier to understand and explain. In the age without computers, Elo ratings can even be calculated by hand. According to this, Elo rating has been used as a common rating system for many different games for a long time. However, compared to the Elo rating system, since a better probabilistic model has been used in WHR, we can usually get a more accurate rating with it. We have the following examples to compare WHR with the Elo rating system.
4.1 Time information
Time information is considered in the WHR system. In the WHR system, it assumes the player rating has a relationship with the time gaps between two games. The longer the time gap is, the greater the player rating will change between two time points.
Let’s see an example. There is a player with a very high rating. Now he plays in a new tournament, but does not perform well. See two different cases:
- The time gap between this new tournament and his last tournament is one month.
- The time gap between this new tournament and his last tournament is several years.
In the traditional Elo rating system, the new rating will be the same with these two cases. But in the WHR system, the new rating in the second case will be much lower than that in the first case. Because after several years, there is a high probability that the rating has a big change.
This situation is common, since there are often some old players who had not played in any tournaments for many years and returned after that.
4.2 Full usage of games
In the traditional Elo rating system, there are players with established ratings and provisional ratings. For games related to provisional players,
- A game between two provisional players has no effect on the ratings. Even if they get their established ratings afterward, this game will not be counted in anymore.
- A game between a provisional player and an established player only has an effect on the rating of the provisional player, but no effect on that of the established player.
In this way, a lot of information is lost for games related to provisional players. Different from this, in the WHR system, all the games will be used to calculate the ratings, no matter whether the players are established or provisional, which makes a more accurate rating evaluation.
Here is an example. In Team World Championship 2012, player Y lost two games to player L. But since player L was a provisional player at that time, these two games were not considered to calculate the rating of player Y. This made player Y’s rating higher than his true strength at that time. The WHR system will correct such a bias by calculating the ratings with all the games.
4.3 Time sequence of games
In the traditional rating system, the latter tournaments have no effect on the rating calculation of the previous tournaments. However, in WHR, the rating calculations of all tournaments are interrelated. Here is an example:
- There are four players, A, B, C and D. They will take two tournaments T1 and T2, and T2 happens after T1. The four players have the same ratings before the upcoming tournaments.
- In tournament T1, A has a draw with C, and B has a draw with D.
- In tournament T2, A has a draw with B, and C wins D.
- There are no other games happening within this time period.
- The question is, who will have a higher rating after T2, A or B?
In the traditional Elo rating system, it is obvious that A and B will have the same ratings after T2. The fact that C wins D in has no effect on the ratings of A and B.
However, in the WHR system, the rating of A will be slightly higher than B after T2. The result that C wins D makes the rating of C higher than D, which also increases the rating of A slightly, according to the result that A has a draw with C and B has a draw with D in T1, in spite of the fact that T1 happens before T2.
4.4 Differences of countries
This idea was proposed by Dmitry Epifanov in the General Assembly of RIF. As we know, most renju tournaments are local, and there are only a few international tournaments, such as the World Championships, which are held every two years. This leads to a problem, that is, for players from different countries, the baselines of their ratings will be different.
In the traditional Elo rating system, since there are more local tournaments and much fewer international tournaments, it is difficult to reach a balanced state between the players from different countries. The ratings will be slightly higher for some countries, and slightly lower for some other countries.
In the WHR system, since we need to update the ratings iteratively for multiple times during the optimization process, it will lower the differences between the rating baselines of different countries. In this way, the ratings of players will become more consistent for different countries.
5. Conclusion
In this article, we have introduced two different rating systems, the classical Elo rating system, and the Whole-History Rating (WHR). We have also compared the differences between them. Welcome to discuss with us and make suggestions if there are any ideas.
References
- Rémi Coulom. Whole-history rating: A Bayesian rating system for players of time-varying strength. In International Conference on Computers and Games. 2008. https://www.remi-coulom.fr/WHR/WHR.pdf
- Arpad E. Elo. The Rating of Chessplayers, Past and Present. Arco Publishing, New York, 1978. https://www.gwern.net/docs/statistics/comparison/1978-elo-theratingofchessplayerspastandpresent.pdf